Ejercicios de aplicación de vectores
Vamos aprender a sumar y restar vectores, por el método gráfico, el analítico y el método de descomposición con ejercicios resueltos y explicados.
Sumar el siguiente sistema de vectores a y b y obtener la resultante grafica y analítica.
Vector a módulo de 5
Vector b módulo de 3
La solución Gráfica sería:
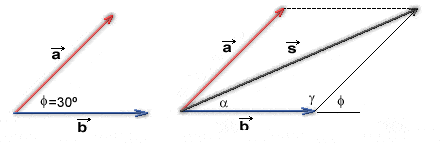
Descomponemos los vectores:
ax = a x coseno 30 = 5 x 0.86 = 4,33
ay = a x seno 30 = 5 x 0,5 = 2,5
bx = 3; solo tiene componente X, no tiene Y.
El vector suma será s = (ax + bx) (ay + by) = (4,33 + 3) ( 2,5 + 0) = (7.33, 2,5) También podríamos verlo expresado de esta forma s = 7,33j + 2,5i
Estas coordenadas son los componentes X e Y del nuevo vector. Si queremos saber su módulo, aplicando Pitágoras será la hipotenusa de ab, o lo que es lo mismo raíz cuadrada del cuadrado de 7,33 + el cuadrado de 2,5.
7,332 + 2,52= 53,72 + 6,25 = 59,67 ===> la raíz será √59,67 = 7,74 que será el módulo de s
Como s y sus componentes forman también un triangulo, calculemos el ángulo que forma por Pitágoras
El ángulo que forma será : coseno ∝ = Sx / S ==> coseno ∝ = 7,33/7,74 = 0,9470
El arco coseno es el ángulo de un coseno. Con una calculadora científica calculamos el arcoseno de 0,9470 y nos dará el ángulo que forma ese coseno. En nuestro caso arcoseno (0,9470) = 18.73 Grados. Este será el ángulo que forma s con la horizontal ∝ (eje X).
Problema Resuelto. Veamos otro ejercicio:
Ejercicio Suma de Vectores
Encuentra en forma analítica las componentes rectangulares de un vector cuyo módulo es de 60 y forma un ángulo de 45º con respecto a la horizontal en sentido noreste.
Datos
α = 450
sen 450= 0.7
cos 450= 0.7
ax ≈ ?
coseno 45º = ax/a; seno 45º = ay/a ==> Despejando las componentes será:
ax= a cos 450
ay= a sen 450
Sustituimos y calculamos
ax= 60 cos 450 = 60∙0.7= 42
ax= 42
ay= 60 sen450 = 60∙0.7= 42
ay= 42
Las dos componentes tendrán el mismo valor. Problema Resuelto.
Sumar el siguiente sistema de vectores a y b y obtener la resultante grafica y analítica.
Vector a módulo de 5
Vector b módulo de 3
La solución Gráfica sería:

Descomponemos los vectores:
ax = a x coseno 30 = 5 x 0.86 = 4,33
ay = a x seno 30 = 5 x 0,5 = 2,5
bx = 3; solo tiene componente X, no tiene Y.
El vector suma será s = (ax + bx) (ay + by) = (4,33 + 3) ( 2,5 + 0) = (7.33, 2,5) También podríamos verlo expresado de esta forma s = 7,33j + 2,5i
Estas coordenadas son los componentes X e Y del nuevo vector. Si queremos saber su módulo, aplicando Pitágoras será la hipotenusa de ab, o lo que es lo mismo raíz cuadrada del cuadrado de 7,33 + el cuadrado de 2,5.
7,332 + 2,52= 53,72 + 6,25 = 59,67 ===> la raíz será √59,67 = 7,74 que será el módulo de s
Como s y sus componentes forman también un triangulo, calculemos el ángulo que forma por Pitágoras
El ángulo que forma será : coseno ∝ = Sx / S ==> coseno ∝ = 7,33/7,74 = 0,9470
El arco coseno es el ángulo de un coseno. Con una calculadora científica calculamos el arcoseno de 0,9470 y nos dará el ángulo que forma ese coseno. En nuestro caso arcoseno (0,9470) = 18.73 Grados. Este será el ángulo que forma s con la horizontal ∝ (eje X).
Problema Resuelto. Veamos otro ejercicio:
Ejercicio Suma de Vectores
Encuentra en forma analítica las componentes rectangulares de un vector cuyo módulo es de 60 y forma un ángulo de 45º con respecto a la horizontal en sentido noreste.
Datos
α = 450
sen 450= 0.7
cos 450= 0.7
ax ≈ ?
coseno 45º = ax/a; seno 45º = ay/a ==> Despejando las componentes será:
ax= a cos 450
ay= a sen 450
Sustituimos y calculamos
ax= 60 cos 450 = 60∙0.7= 42
ax= 42
ay= 60 sen450 = 60∙0.7= 42
ay= 42
Las dos componentes tendrán el mismo valor. Problema Resuelto.
Comentarios
Publicar un comentario