Métodos para la resolución de vectores
Método del paralelogramo
Para hacer una suma de vectores gráficamente por este método, se trazan los dos vectores desde el mismo origen y se forma un paralelogramo usando los vectores como lados adyacentes, el vector resultante es la diagonal que se traza desde el origen.
Ejemplo:
Tenemos los siguientes dos vectores:
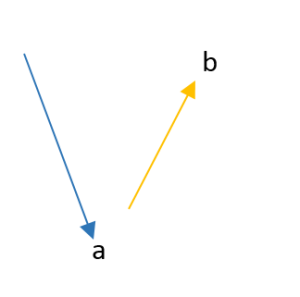
Trazamos los dos vectores desde el mismo origen:

Para hacer una suma de vectores gráficamente por este método, se trazan los dos vectores desde el mismo origen y se forma un paralelogramo usando los vectores como lados adyacentes, el vector resultante es la diagonal que se traza desde el origen.
Ejemplo:
Tenemos los siguientes dos vectores:

Trazamos los dos vectores desde el mismo origen:

Hacemos lineas paralelas a cada vector para formar un paralelogramo:
El vector resultante a+b será la línea diagonal que sale desde el origen:

Método del triángulo
Método del polígono
Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.
El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.
Ejemplo. Sean los vectores:
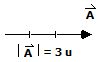
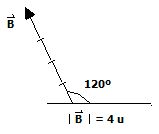
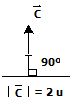
Encontrar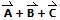 .
.
Resolviendo por el método del polígono, la figura resultante es: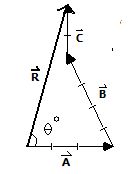
Si se utilizan los instrumentos de medición prácticos, se obtiene que :
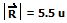
y que θ es aproximadamente 80ª.
Cuando dos vectores se restan, el procedimiento anterior es el mismo, lo único que cambia es el sentido del vector que le sigue al signo menos. Por ejemplo, al restar el vector D2 del vector D1 se tiene:
D1- D2 = D1+ (-D2).
La expresión del miembro derecho de la ecuación anterior designa un cambio en el sentido del vector D2; entonces, la expresión queda como una suma, y por lo tanto, se sigue el procedimiento del método gráfico mostrado anteriormente.
Los métodos gráficos ofrecen una manera sencilla de sumar o restar dos o más vectores; pero cuando las magnitudes de los vectores son demasiado grandes o poseen una gran cantidad de decimales, éstos métodos se vuelven imprecisos y difíciles de manipular a escalas de medición menores.
Es por eso, la necesidad de un método matemático nemotécnico, que permita dar una mayor precisión en el cálculo de vectores resultantes, no sólo en la magnitud, sino además en la dirección de ellas.
El vector resultante a+b será la línea diagonal que sale desde el origen:

Método del triángulo
Este método consiste en referir un vector en un plano cartesiano, en el punto final del mismo trazar un nuevo plano cartesiano y aplicar el segundo vector, el vector resultante o vector suma, se definirá del punto de origen del primer vector al punto final del segundo vector. Ejemplo:
Teniendo: y , hallar
La intensidad o magnitud y la dirección de la resultante se obtendrán realizando la medición de ambas magnitudes directamente en la gráfica o dibujo realizado.
Método de paralelogramo.
En este método se refieren los dos vectores al mismo sistema de coordenadas, posteriormente se sacan líneas auxiliares, las cuales son paralelas a cada vector pero iniciando en el vector opuesto, él vector suma o resultante se generará del punto de origen de los dos vectores al punto de intersección de las líneas auxiliares.
Nos sirve para sumar dos vectores simultáneos.
1.-Consiste en dibujar los dos vectores a escala con sus orígenes coincidiendo con el origen.
2.-Los vectores forman de esta manera los lados adyacentes de un paralelogramo, los otros dos lados se construyen dibujando líneas paralelas en los vectores de igual magnitud.
3.-La resultante se obtendrá de la diagonal del paralelogramo a partir del origen común de los vectores.
Método del polígono
Éste es el método gráfico más utilizado para realizar operaciones con vectores, debido a que se pueden sumar o restar dos o más vectores a la vez.
El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.
Ejemplo. Sean los vectores:
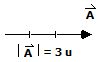
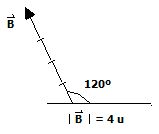

Encontrar
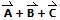 .
.Resolviendo por el método del polígono, la figura resultante es:

Si se utilizan los instrumentos de medición prácticos, se obtiene que :
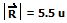
y que θ es aproximadamente 80ª.
Cuando dos vectores se restan, el procedimiento anterior es el mismo, lo único que cambia es el sentido del vector que le sigue al signo menos. Por ejemplo, al restar el vector D2 del vector D1 se tiene:
D1- D2 = D1+ (-D2).
La expresión del miembro derecho de la ecuación anterior designa un cambio en el sentido del vector D2; entonces, la expresión queda como una suma, y por lo tanto, se sigue el procedimiento del método gráfico mostrado anteriormente.
Los métodos gráficos ofrecen una manera sencilla de sumar o restar dos o más vectores; pero cuando las magnitudes de los vectores son demasiado grandes o poseen una gran cantidad de decimales, éstos métodos se vuelven imprecisos y difíciles de manipular a escalas de medición menores.
Es por eso, la necesidad de un método matemático nemotécnico, que permita dar una mayor precisión en el cálculo de vectores resultantes, no sólo en la magnitud, sino además en la dirección de ellas.
Método de las Componentes
Éste método mejora la precisión y la rapidez al determinar el vector resultante por medio del conocimiento de las componentes del vector; además tiene la ventaja de sumar o restar dos o más vectores a la vez, mediante un proceso algebraico.
El método consiste en sumar o restar las componentes en x de los vectores principales, y el resultado de ésta operación es la componente en x del vector resultante.
De igual manera, se operan las componentes en y de los vectores principales y el resultado es la componente en y del vector resultante.
Obtenidas las componentes de la resultante, se pueden encontrar la magnitud, dirección y sentido de éste vector.
Cuando una componente, en x o en y, tiene un valor negativo, el sentido de ésa componente es contrario a los lados positivos del marco de referencia. Por ejemplo, si una componente en y tiene un valor negativo, la proyección en el eje y de ése vector apunta hacia abajo.
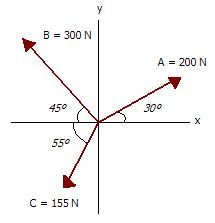
Ejemplo. Calcule la resultante de las fuerzas que se presentan en la figura.
Note que θ para los vectores B y C no son los que se presentan en la figura, sino que se deben calcular a partir del eje x positivo (ángulos suplementarios).
Para el vector B, θ = 180º - 45º = 135º
Para el vector C, θ = 180º + 55º = 235º
Calculando las componentes en x de los vectores A, B y C:
Ax = (200 N) cos (30º) = 173.20 N
Bx = (300 N) cos (135º) = - 212.13 N
Cx = (155 N) cos (235º) = - 88.90 N
Calculando las componentes en y de los vectores A, B y C:
Ay = (200 N) sen (30º) = 100 N
By = (300 N) sen (135º) = 212.13 N
Cy = (155 N) sen (235º) = - 126.97 N
Luego se calcula la fuerza resultante, encontrando las componentes de ésta fuerza, a partir de una simple suma de componentes de fuerzas individuales.

Comentarios
Publicar un comentario